Logika rozmyta (ang. fuzzy logic), jedna z logik wielowartościowych (ang. multi-valued logic), stanowi uogólnienie klasycznej dwuwartościowej logiki. Jest ściśle powiązana z teorią zbiorów rozmytych i teorią prawdopodobieństwa. Została zaproponowana przez Lotfi Zadeha w 1965 roku. W logice rozmytej między stanem 0 (fałsz) a stanem 1 (prawda) rozciąga się szereg wartości pośrednich, które określają stopień przynależności elementu do zbioru, logika taka ma jednak skończoną liczbę wartości.
Logika rozmyta okazała się bardzo przydatna w zastosowaniach inżynierskich, czyli tam, gdzie klasyczna logika klasyfikująca jedynie według kryterium prawda/fałsz nie potrafi skutecznie poradzić sobie z wieloma niejednoznacznościami i sprzecznościami. Znajduje wiele zastosowań, między innymi w elektronicznych systemach sterowania (maszynami, pojazdami i automatami), zadaniach eksploracji danych czy też w budowie systemów ekspertowych .
Metody logiki rozmytej wraz z algorytmami ewolucyjnymi i sieciami neuronowymi stanowią nowoczesne narzędzia do budowy inteligentnych (nie mylić ze świadomymi) systemów mających zdolności uogólniania wiedzy.
Logika wielowartościowa
Logika wielowartościowa to rodzaj rachunku zdań, w którym przyjmuje się więcej niż dwie wartości logiczne.
Tradycyjny rachunek zdań jest dwuwartościowy – są w nim możliwe tylko dwie wartości logiczne – prawda albo fałsz (co odpowiada podstawowej intuicji związanej z prawdziwością wypowiedzi). Jednakże klasyczna dwuwartościowość jest tylko jedną z możliwości zakresu wartości logicznych. Możliwe są logiki w których istnieją inne wartości logiczne lub nawet takie w których występują więcej niż dwie wartości.
W klasycznym ujęciu logiki zdanie może przyjmować alternatywnie jedną z dwóch wartości – „prawda” albo „fałsz”. Jeżeli zdanie nie posiada jednej z tych właściwości, to automatycznie posiada drugą. Jest to treścią prawa wyłączonego środka.
Należy zauważyć, że istotą rachunku zdań są takie przekształcenia zdań, które zachowują dla nich pewne własności. W klasycznej logice taką własnością jest „prawda”. W poprawnym rozumowaniu zdanie ostatecznie otrzymane na drodze przekształceń zdania prawdziwego, zachowujących prawdziwość, także jest prawdziwe.
Jednak „prawdziwość” może być zastąpione inną ideą. Na przykład w logice intuicjonistycznej jest nią „uzasadnienie”. Zdanie może wtedy posiadać jedną z dwóch cech: może być „uzasadnione”, bądź nie. Istotną różnicą między „prawdą”, a „uzasadnieniem” jest to, że dla tego ostatniego nie zachodzi prawo wyłączonego środka: zdanie które nie jest nieuzasadnione niekoniecznie musi być uzasadnione. W takim przypadku jedynie nie zostało udowodnione jego uzasadnienie. Oznacza to, że można udowodnić, że P jest uzasadnione, że P nie jest uzasadnione, bądź nie można dowieść żadnego z powyższych. Poprawne rozumowanie zachowuje uzasadnienie zdań, więc zdanie wywiedzione z uzasadnionego zdania jest wciąż uzasadnione. Jednak istnieją dowody, które wymagają zastosowania prawa wyłączonego środka – w takim przypadku istnieją zdania, które nie mogą być uzasadnione.
Logikę rozmytą po raz pierwszy przedstawił Lotfi Zadeh jako formalizację niepewności, to jest zjawiska występowania obiektów wobec których pewne określenia stosują się tylko w pewnym stopniu.
Historia
Pierwszym logikiem, który nie w pełni zgadzał się z prawem wyłączonego środka był Arystoteles (De Interpretatione, ch. IX), jednak nie wyprowadził on pełnego, wielowartościowego systemu logicznego. Prawo to było w pełni akceptowane przez stoików (może ono pochodzić od jednego z nich). Późniejsi logicy, aż do lat dwudziestych dwudziestego wieku podążali za Arystotelesem, nie rozważając jednak prawa wyłączonego środka. Nieco inaczej sytuacja prezentowała się w indyjskich systemach filozoficznych np. Nagardżuna (II w n.e.) przedstawił dwuwartościową logikę czterech alternatyw, na bazie której opracował system filozoficzny Środkowej Ścieżki (madhyamaka).
W wieku dwudziestym idea logiki wielowartościowej powróciła. Polski logik i filozof Jan Łukasiewicz tworzył wielowartościowe systemy logiczne od 1920 roku, używając jako trzeciej wartości logicznej – „możliwe”. W tym samym czasie amerykański matematyk Emil Post także sformułował ideę dodatkowych wartości logicznych. Kurt Gödel w 1932 pokazał, że logika intuicjonistyczna nie jest logiką o skończonej liczbie wartości logicznych i sformułował logikę Gödla, leżącą pomiędzy logiką klasyczną, a intuicjonistyczną. Logiki o tej własności nazywane są Logikami pośrednimi.
Zbiór rozmyty
Zbiorem rozmytym A w przestrzeni X jest zbiór uporządkowanych par:
gdzie ![\mu_A\colon X \to [0,1].\](https://www.inguaris.pl/wp-content/uploads/2021/11/f1b31b0f9372d1e169d26a7da81c4f5b.png)
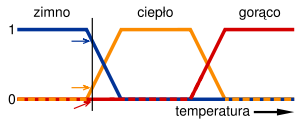
Przykładem zbioru rozmytego może być „zbiór wysokich ludzi”. Oczywiście niektórzy ludzie są wysocy (przynależność 1,0), inni zaś nie są (przynależność 0,0), jest jednak duża grupa ludzi pomiędzy tymi dwiema skrajnościami, dla których funkcja przynależności przyjmuje wartości pośrednie.
W teorii zbiorów rozmytych używane są różne funkcje przynależności. Najczęściej stosowane to funkcja trapezowa, trójkątna i tak zwana s-funkcja.
Ze zbiorem rozmytym związane są następujące wielkości:
- nośnik (ang. support) zbioru rozmytego A – zbiór elementów x, dla których μA(x) > 0;
- rdzeń (ang. core) zbioru rozmytego A – zbiór elementów x, dla których μA(x) = 1;
- wysokość (ang. height) zbioru rozmytego A – największa wartość funkcji przynależności;
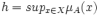 .
.
Zbiór rozmyty jest znormalizowany, wtedy i tylko wtedy, gdy h = 1.
Zbiór rozmyty jest wypukły, wtedy i tylko wtedy, gdy dla dowolnych spełniona jest zależność:
spełniona jest zależność: 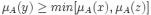 .
.
Na zbiorach rozmytych zdefiniowane są podobne relacje, co na klasycznych zbiorach. - relacja równości:
- relacja zawierania:
Algorytm ewolucyjny
Algorytm ewolucyjny – heurystyczny algorytm optymalizacyjny, zazwyczaj zrandomizowany. W większości algorytmów ewolucyjnych początkowo losuje się zbiór rozwiązań dopuszczalnych (zwanych osobnikami), a następnie poprawia się je za pomocą operatorów ewolucyjnych (jak mutacja, krzyżowanie, selekcja).
Algorytm ewolucyjny operuje na populacji osobników. Populacje krążą w cyklu reprodukcji populacji rodzicielskiej na populację potomną, operacji genetycznych na populacji potomnej, oceny osobników względem zadanego środowiska i sukcesji osobników potomnych do populacji rodzicielskiej. Po wielokrotnej iteracji tego cyklu otrzymujemy, z reguły, osobniki coraz lepiej przystosowane do środowiska.
Wyróżnia się kilka klas algorytmów ewolucyjnych: algorytm genetyczny, strategia ewolucyjna, programowanie genetyczne i programowanie ewolucyjne.
Lotfi Asker Zadeh właściwie Lotfi Aliaskerzadeh (ur. 4 lutego 1921 w Baku, Azerbejdżan), automatyk amerykański.
Studiował na Alborz High School oraz Tehran University, przeniósł się do USA w 1944. Pracownik Kalifornijskiego Uniwersytetu w Berkeley od 1959 roku.
Głównym zagadnieniem, którym się zajmował jest soft computing. Twórca teorii zbiorów rozmytych (fuzzy set, 1965) i logiki rozmytej (1973). Zainteresowania naukowe: sztuczna inteligencja, logika, lingwistyka, teoria sterowania, systemy ekspertowe i sieci neuronowe.
Jest członkiem IEEE, AAAS, ACM, AAAI, and IFSA. Otrzymał wiele doktoratów honoris causa, w tym w Polsce od Politechniki Śląskiej w Gliwicach. Jest laureatem Medalu Hamminga (1992).